Matrix Multiplication

Matrix multiplication why and how

Why matrix and its multiplication is so important in neural network

In the previous post of xor problem, we introduce the network of 2 inputs nodes, 2 hidden nodes and 1 output as the following:

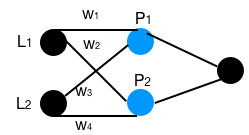
We calculate the values of P1 & P2 as following:

\[\begin{cases} W_1 * L_1 + W_3 * L_2 = P_1 \\ W_2 * L_1 + W_4 * L_2 = P_2 \end{cases}\]

The linear functions is exact the format of matrix multiplication as following:

\[\begin{pmatrix} W_1 & W_3 \\ W_2 & W_4 \end{pmatrix} * \begin{pmatrix} L_1 \\ L_2 \end{pmatrix} = \begin{pmatrix} P_1 \\ P_2 \end{pmatrix}\]

Every matrix represents some linear function, and every linear function is represented by a matrix. That’s the strong connection between the linear function and matrix. In linear space, matrix multiplication represents linear transformation, i.e. a movement in space. The first matrix {w} means movement, the second matrix {L} is the basis, the third {P} is the new location.

So in linear space, the network represents through a set of transformation, the original input outputs the result we expect to, either classification problem or regression problem.

Matrix is a perfect tool for neural network computation. Let’s say the network now goes to 4 hidden nodes as below:

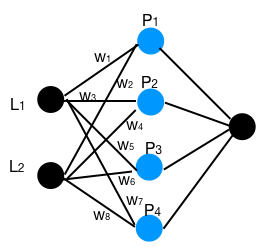
Without the magic matrix, we will need to implement the values for P1 to P4 in 4 functions manually:

\[\begin{cases} W_1 * L_1 + W_2 * L_2 = P_1 \\ W_3 * L_1 + W_4 * L_2 = P_2 \\ W_5 * L_1 + W_6 * L_2 = P_3 \\ W_7 * L_1 + W_8 * L_2 = P_4 \end{cases}\]

When network grows to thousands plus in real practice, the linear function grows accordingly. While with matrix multiplication, the piece of code remains the same:

Matrix hidden_layer = Matrix weights * Matrix input

As matrix is widely used in machine learning, there are good amounts of existing libraries about matrix operation. Below is the matrix multiplication in processing, as we really want to build a neural network from scratch, we implemented a simple matrix library as well:

Matrix multiply(Matrix a, Matrix b) {
  // matual product
  if (a.cols != b.rows) {
    return null;
  }
  Matrix result = new Matrix(a.rows, b.cols);
  for (int i = 0; i < a.rows; i++) {
    for (int j = 0; j < b.cols; j++) {
      float sum = 0;
      for (int k = 0; k < a.cols; k++) {
        sum += a.data[i][k] * b.data[k][j];
      }
      result.data[i][j] = sum;
    }
  }
  return result;
}

This could work in demo usage, while if we look into the codes, we will find there are nested loop with 3 “for”，the asymptotic complexity is $O(N^3)$ for 2 matrices in same dimension.

How to code in a more efficient way for multiplication

With the Strassen algorithm, the asymptotic complexity could be squeezed to $O(N^{log_27})\approx O(N^{2.8074})$. I don’t have better explanations than wikipedia on Strassen algorithm

[post status: pending]