Volume of Cone [series 1]

Volume of Cone

series 1: Volume of Cone

We will calculate volumes by cross sections with helps of definite integral.

Let’s first look at the type of cross section in horizontal:

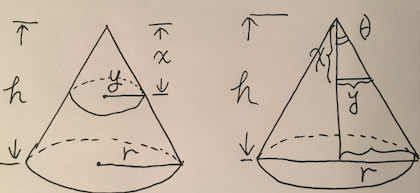
Let’s denote radius of cross section of “y”, now we are going to figure out formula of it:

\[\tan\theta = \frac yx = \frac rh\] \[y = \frac rh * x\] \[\int_{x=0}^{x=h}\pi(\frac rh * x)^2dx = \pi(\frac rh)^2\int_{x=0}^{x=h}x^2dx\] \[V = \pi(\frac rh)^2\frac {h^3} {3} = \frac 13\pi r^2h\]

The above procedure seems nice & neat.

Now let’s challenge ourselves by asking:

Why should us calculate the volume by figuring out the “y”, instead of “x”?

Or, why shouldn’t calculate by cross sections of vertical?

\[\tan\theta = \frac xy = \frac hr\] \[x = \frac hr * y\] \[\int_{y=0}^{y=r}\frac 12 * y * \frac hr * y * 2 * 2 = 2 (\frac hr)\int_{y=0}^{y=r}y^2dy\] \[V = \frac 23 * h * r^2\]

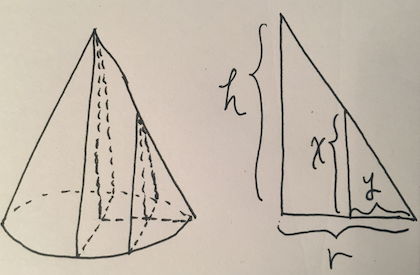
Compare with previous one:

\[\frac 13 \pi r^2 * h \neq \frac 23 * h * r^2\]

So, where is the error?

Following is the cite of Conic Section from wikipedia:

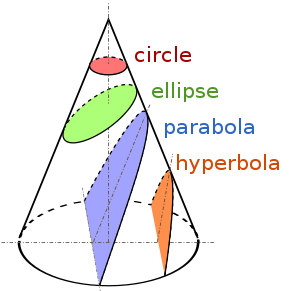
So do not mislead by the previous wrong infer, the vertical section is hyperbola instead of triangle.

Or think in this way:

We are actually calculating the volume of a pyramid, just thinking the radius of “r” is a special case of a pyramid:

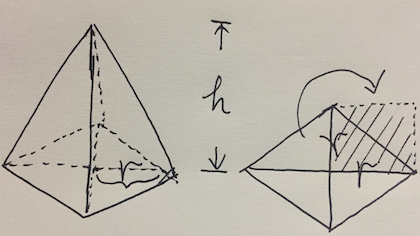
We may get the area of pyramid the above case is: “ r * r * 2 “. So the volume turns from:

\[\frac 23 h r^2\]

into:

\[\frac 13 h S\]

in which S is the area of bottom of pyramid, it’s also the formula of volume of pyramid.

Math is fun.~~~~

[post status: almost done]