Neural Network [grade 1]

Neural Network: single perceptron

grade 1: single perceptron

It’s the initial post of series: neural network.

The languages will be implemented here are: javascript/python and processing.

Reason for choosing these 2, is they are easy to visualize and provides friendly interaction, which will help out in understanding “how”.

I believe in make “something” visible requires comprehensive understanding on “something”.

Won’t start from introduction of neuron & brain science etc, as these staffs could be easily get online. Instead, let’s start by neuron from machine learning perspective.

Neural network has wide usage in all sorts of machine learning scenarios. As skyscraper was made of tiny bricks, the neural network was made of “perceptrons”.

Following is the diagram of simplest and basic unit of network, a processor. With millions even billions of perceptrons communicate to each other, a sophisticated system was built on top of it.

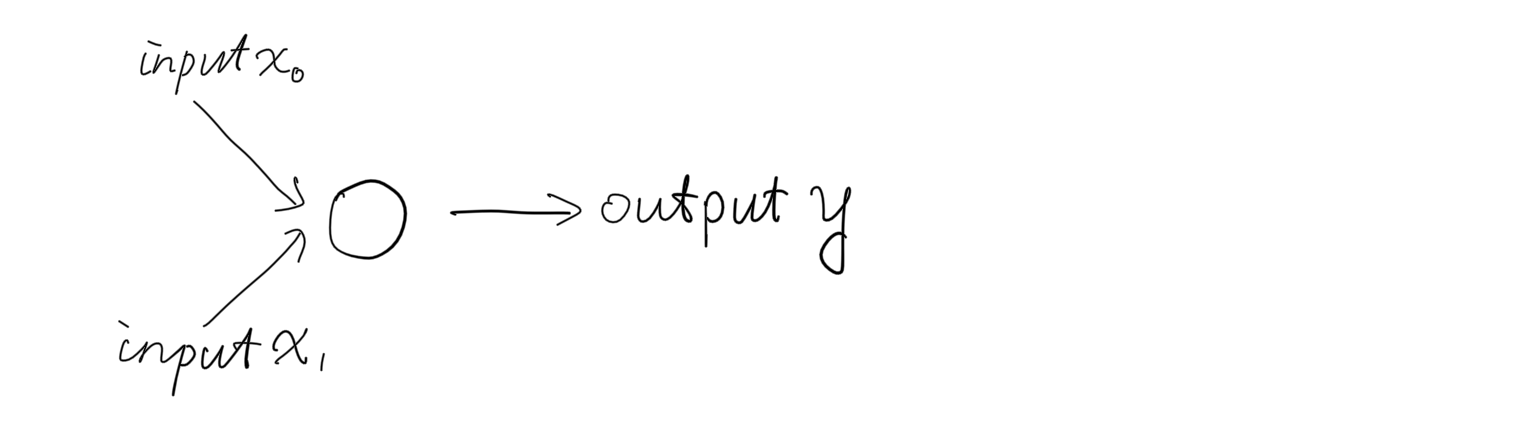
 The target of grade 1: to build a linear classifier , which could classify 2 categories in a 2 dimension space.

What’s the basic functionality of a neuron , aka perceptron in machine learning terminology. Typically, a perceptron takes in inputs, sum up them, according to a “predefined” rule of judge, outputs a setting value.

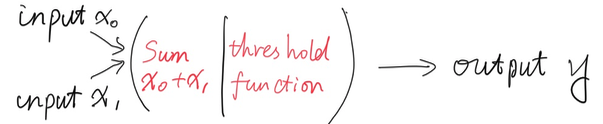
Here, a perceptron could take in thousands and even more inputs, i.e. in image classification scenarios. While use 2 inputs here, other than simplify the scenario, 2 inputs could be project to a 2 dimension space x value and y value, which makes it easier for us to visualize.

First, let’s achieve our initial target, make a workable perceptron, just like the 1st cell in biological evolution.

As a perceptron, 2 main functionalities: step 1. sum up input values according its weights step 2. sign inputs and generate outputs of -1 and 1

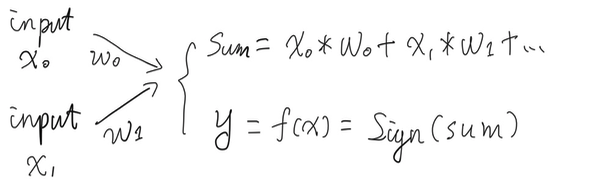
Let’s start implement some codes here, following are the core codes in processing:

class Perceptron {
  float[] weights;
  float learning_rate = 0.01; // a random picked value

  // Constructor, takes in # of weights and initialize
  Perceptron(int n) {
    weights = new float[n];
    for (int i = 0; i < weights.length; i++) {
      weights[i] = random(-1, 1);
    }
  }

  // Generate outputs
  int predict(float[] inputs) {
    float sum = 0;
    for (int i= 0; i < weights.length; i++) {
      sum += inputs[i] * weights[i];
    }
    int predict = sign(sum);
    return predict;
  }

  // Activate function, sign is a basic function gets "+" / "-"
  int sign(float sum) {
    if (sum >= 0) {
      return 1;
    } else {
      return -1;
    }
  }

}

How does a perceptron work, just as following:

Perceptron nn;

void setup() {
  size(400, 400);
  nn = new Perceptron(2);
  float inputs[] = {0.5, -1};
  // with bias version, there will be 3 inputs and 3 weights accordingly
  /*
  nn = new Perceptron(3);
  float inputs[] = {0.5, -1, 1}; // we give default value of bias: 1
  */
  int predict = nn.predict(inputs);
  println(predict);
}

void draw() {
}

Simply like that.

Codes on github https://github.com/hifreedo/nnfs

Math been invoked in this grade

sum = w0*x0 + w1*x1 + ...
sign

Cite from wikipedia:

Sign of a number. Every number has multiple attributes (such as value, sign and magnitude). A real number is said to be positive if its value (not its magnitude) is greater than zero, and negative if it is less than zero. The attribute of being positive or negative is called the sign of the number.

We will discuss the scenario of been zero now: With the equation: sum = weightX, let’s try to simplify it into: y = wx, we may encounter with y = 0 when weight or x is zero. And to 0, the sign in strict definition actually could not apply, thus positive or negative could not be generated.

As we know, with equation: y = w*x, which could only generate a line cross through the coordinate (0, 0).

As y = w*x + b is the real universal equation that could draw any line from any direction is a 2D dimension, here we could simply add “another” input to the neuron network structure, which is called the “bias”. Which is a fixed number in practical and has its weight as well. Hence, the equation for sum up values with perceptron turns into: sum = weight *x + weight * bias

As bias usually takes “1” as value, by doing this, we eliminate the impact of sum to be zero and developed a universal 2D linear classification function: y = w*x + b. Which will be implemented in detail in grade 2:

To be continued in Grade 2

Let’s see what does a “neuron” really get. We will come up with a scenario, commence a classification problem: linearly split a 2D space.

[post status: almost done]